用語解説 一覧
キラル(chiral)の語源は、ギリシャ語の「手」や「掌」を意味するcheirに由来するものと考えられている。名詞形はキラリティ(chirality:掌性)であるが、キラリティではない形に対して、アキラル(achiral)という形容詞表現がある。これに由来する語は、一般に広く伝承されておらず、わずかに類似の語としてchirography(筆跡)、chirology(手話法)、chirognomy(手相術)などに痕跡が認められる。他方、「脊柱指圧」のことをchiropracというが、これも「手」に関係して発達した語と推定される。また、外科医を英語では、surgeonと言うが、ドイツ語ではchirurgといいい、これも同系の言葉であろう言われている(1)。
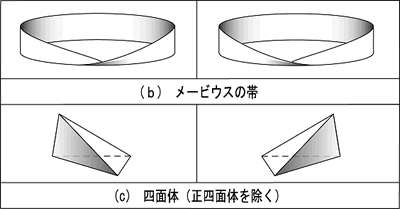
さて、キラル媒質とは、通常の誘電媒質にキラル物体を埋め込むことによって構成され、キラル物体とは、それ自身とその鏡像体が平行移動や回転移動によっても合同にはならない物体であると定義されている(2),(3)。例として、図に示すような、らせん導体やメービウスの帯,四面体などが知られている。特徴としては、この媒質に直線偏波した平面電磁波が入射すると、媒質中の電磁界は位相速度の異なる右回り円偏波と左回り円偏波との重ね合わせによって表される直線偏波となり、これは光学活性体と同様な性質を示す(2), (3)。
- (1)竹本喜一, 金岡喜久子:“化学語源ものがたり” 化学同人, 1986.
- (2)田中充, 佐藤一政:“層状キラルスラブの透過および反射特性” 電子情報通信学会論文誌C-I Vol.J75-C-I No.10, 1992.
- (3)Nader Engheta, Dwight L. Jagggard:“Electromagnetic Chirality and Its Applications” IEEE Antennas and Plopagation Society News-letter, October, 1988.
キラルとかキラリティという言葉は、グラスゴー大学の物理学者William Thompson(Lord Kelvin)がジョンズホプキンス大学で1884年10月17日に使ったのが最初であるといわれている。1966年にCahn, IngoldとPrelogが分子不斉の記述に関する古典的な論文を書いて以来、これらの術語が普及ししてきた。キラル(およびアキラル)は、幾何学的な図形ないしは模型に適用した際に正確な意味をもっている。しかし、分子、溶媒、試薬などの実在する系では、それほど明確ではなく、測定条件に依存すると指摘されている(1)。
- (1)A. Nickon, E. F. Silversmith 共著, 大澤映二 監訳:“化学者たちのネームゲーム ?名付けた親たちの語るドラマ?” 化学同人, 1991.
メタマテリアルは,自然界には存在しない人工的に制作された材料を意味している。とくに電磁波用途の人工 材料は、Electromagnetic Metamaterials のように記され、誘電率( εr ),透磁率( μr )が取り得る正,負の値によって,大きく2 種に分類される。一つは,(ⅰ)誘電率, 透磁率が同時に負の値を取り,電磁波に対する屈折率が負となる「左手系材料(Left-handed Metamaterials)」と呼ばれるものである。他は,(ⅱ)誘電率, 透磁率が同 時に負の値を取らぬ材料群に属する広義な意味における人工材料を含めたものを「右手系材料(Right-handed Metamaterials)」と呼んでいる。また,媒質として表現する場合は,「左手系媒質(Left-handed Medium)」,「右手系媒質(Right-handed Medium)」のように記される。
電波吸収体とは、到来した電波を吸収して熱に変換したり、到来波の位相を相殺したりする原理で、反射波を生じさせないように構成されている物体のことである。
電波吸収体を世界で初めて実際に使用したのは、第二次大戦中のドイツ軍であったと言われている。ドイツ軍が誇った潜水艦(U-Boat, Unterseeboot)が、海面から潜望鏡を出しているところを対潜哨戒機のレーダで捕捉されないように、この潜望鏡をレーダ電波から無反射にする方策が考えられた。つまり電波吸収体の必要性が考えられるようになったのである。ここで利用された電波吸収材は、現在でも使われているカーボンブラックを含む材料で、これを潜望鏡に巻き付けることで効果を挙げたと言われている。その後、電波吸収体は電波を反射しない空間、つまり電波暗室を実現するための内壁面材として使われたり、ビル壁面用材料として、テレビゴースト防止対策用ビル壁面用材料とし利用されたりしながら発達し、現在では、レーダ偽像防止対策、移動体通信環境対策、各種電磁障害防止用など幅広く応用されている。
電波吸収体の電波を吸収する割合を示す定量的な値として、通常デシベル表示した反射係数が用いられる。どの程度の値をもって電波吸収体とするかというはっきりした定義はとくに定まっていない。通常の電波吸収体では、-20[dB]を基準とし、これ以下の値をとることをもって電波吸収体と称することが多い。この-20[dB]という値は、電界反射係数で0.1、電力反射係数では、0.01に相当し、電波吸収体に入射した電波エネルギーのうち99%が吸収される状態に当たる。従来、電波吸収体の吸収量は電圧定在波比 (Voltage Standing Wave Ratio)で評価されてきたが、現状では、上述の反射係数がよく使われている。また最近、単に反射量(reflectivity )と呼ばれる傾向にもある。-20[dB]は、VSWR値では1.2に相当している。ちなみに、反射係数-30[dB]では、吸収体に入射したエネルギーのうち、99.9%が吸収される。
反射係数には、入射電力Piに対する反射電力Prの割合を示す電力反射係数Pi / Prと、入射電界Eiと反射電界Erで表した電圧反射係数Er /Eiがある。電波吸収体の吸収能力を表す量表現は現在様々な呼称で使われており、反射係数はじめ、反射量、反射減衰量、リターンロスなどと呼ばれている。
電波吸収体を吸収することが出来る材料はさほど多くない。構成材料で分類すると(1) 導電性電波吸収材、(2) 誘電性吸収材、(3) 磁性電波吸収材、(4) メタマテリアルによる電波吸収材などに分類できる。
- (1)はカーボンブラック、グラファイト等の炭素系材料を基材として構成された抵抗体を用いるもので、高周波電流が、ジュール熱に変換されて電波を吸収するタイプである。
- (2)は、主として上述の炭素系の材料を発砲ウタレン、ゴム材等に混入して構成した電波吸収体で、電界に対して効果的作用して電波を吸収するタイプである。
- (3)はフェライトに代表される電波吸収体で、フェライトとしては、通常、焼結フェライト、ゴムフェライト、プラスティックフェライトなどが用いられている。
- (4)は、近年注目され始めた人工材料、メタマテリアルからなるもので、広義な意味におけるメタマテリアルと称する媒質で構成する電波吸収体が提案されている。基本的には、非磁性金属材料だけで誘電率や透磁率を実現したものや、能動素子によって電波吸収体部分を構成したものなどがある。
誘電加熱とは、被加熱体としての誘電体(絶縁体)に高周波の電界を加えて、高周波電界による誘電体損を利用して、被加熱体を発熱させる方法である。
通常、誘電体内の原子や分子は、原子、分子間結合力によって束縛されており、高周波電界を加えると、この結合力による抵抗を受ける。したがって、高周波電界を誘電体に加えると、エネルギー損失が生じ、この損失分が熱の形で現れると考えられている。この現象は、誘電体の「分極」と深く関わっている。
誘電加熱は、適用周波数が低周波であるか、高周波であるかによって、加熱機構が異なり、大きくRF誘電加熱、マイクロ波誘電加熱に分類される。誘電、誘導両加熱法は、従来、木材乾燥、熱硬化性プラスチックの成型加工、生ゴムの加硫など工業応用をベースに発展してきたが、近年、生体応用も進み、癌の温熱療法などにも応用されている。
誘導加熱は、損失を有する導体が交番磁界中に置かれていると、うず電流が発生し、ジュール損に基づく発熱が起こるという原理を応用した加熱法である。うず電流は、導体内部を交番磁界が貫くとき、ファラデーの電磁誘導法則に基づく起電力によって、うず状に流れる電流である。したがって、通常の抵抗をもっている導体にうず電流が発生すれば、ジュール損失による発熱として現れる。工業応用としては、金属表面に焼き入れを施せば表面強度が増すことからで、自動車部品など多く強度を必要とする部品類にこの誘導加熱が使われている。その他、高周波ロー付けや、鍛造への応用、歯車製造など他、生体応用として、がん温熱療法への研究も進んでいる。
コードセンシング通信方式(Code-Sensing Communication System;COSCOS)とは、基本的には「バーコード」のようなコード情報を、光や微弱電磁波などをセンシング手段として用いコードをセンシングし、あらかじめ受信側装置に記憶されているメモリ情報と照合し、情報を音声や画像で提供する簡易な通信方式と定義される。センシング方式は、磁気式センサ式、画像処理式、多周波列放射型コードセンシング式、光学式コードセンシング式、超音波式等に分類される。
この通信方式は、次のような、特徴を備えている。
- 〇局所的な通信を実現できるため、電波の有効利用の点から望ましい方法である。
- 〇光や超音波など無誘導性通信を実現できるため、EMCの観点からも有効な方法と考えられる。
- 〇複数のコードの列で表示されるコード情報表示領域は、至って狭く構成でき、センサでコードを読み取った後、受信側のメモリにあらかじめ記憶させてある内容と照合し、最終的に画像や音声レベルの高出力によって、利用者に対する必要な情報や移動体制御情報を多く提供することが出来る。
- 〇最近のメモリ技術の進歩から大きなメモリ容量が安価となり、簡単なコード情報から、実際には多くの情報を提供できるという合理性がある。
- 〇時々刻々変動する情報が伝送可能である。
- 〇移動体通信に有効で、移動体が、一旦停止しても移動開始によって情報を検出でき、とくに超高速移動体通信に有効である。
FDTD法(Finite Difference Time Domain Method ) は、マクスウェルの方程式を差分(Finite Difference)化表示して、時間領域(Time Domain)で解く方法である。英語訳と必ずしも対応しないが、通常「時間領域差分法」といわれ、近年、電磁波領域などの研究において有力な解析手段となっている。
従来、電磁界解析の基本的は、ラプラスの方程式やポアソンの方程式を境界条件の下に解く解析的な方法が中心であった。しかし、解析対象によってはこれらの偏微分方程式を解くことは極めて困難となる場合が多い。このような問題解決に対して、コンピュター支援によって、電磁界問題を解く方法が考えれている。これは変分法の考え方に立つ有限要素法が考えられている。有限要素法は、変分法の考え方を基本にしているが、通常ポテンシャルに関する偏微分方程式を汎関数という積分形式で表し、解析対象領域を有限の要素に分割して、その各接点におけるポテンシャルをコンピュタ解析する方法である。各接点のポテンシャルが定まれば、接点間、要素内のポテンシャルは内挿法などで求めることが出来る。
空間回路網法は、まずマクスウェルの方程式導出原理に基づき、離散的な電磁界変数(例えば、(Ex,Ey,Ez), (Hx,Hy,Hz)など)によって表示された3次元格子網モデルを導入する。そして、この格子網の隣接格子節点間を等価的な伝送線路に転換し、これらの格子点間で、空間的、時間的に離散化された電圧、電流表示式を得るためにベルジェロン法を適用する。この等価回路網の各接点(各格子点)で、電流(または、磁流)連続条件を課し、電圧(または、電流)に関する接点方程式を求め、この式を用い電磁界の時間応答解析を行うものである。
これは新しい電波吸収体構成概念として提案された統一概念で、電波吸収材が本来所有している材料定数を、種々の手段で等価的に変換して、所望の電波吸収特性を実現する方法である。これを「材料定数等価変換法」と称している。たとえば電波吸収材に各種形状の空孔を設けて、本来の整合周波数を高周波側へ移行調節する方法、従来の電波吸収材と種々の導体素子層を組み合わせる方法や、高周波集積回路概念に立つ電波吸収体、3次元構造の単位セルと称する各種受動および能動回路素子からなる基本セルを,結晶体の空間格子配列(ブラベー格子配列)に従って構成した「自律制御型メタマテリアル」を用いて、誘電率、透磁率を電気的に制御して等価変換をする方法などがある。
Maxwell-Wagnerの不均質理論と呼ばれるものは、誘電体が不均質媒質、つまり誘電率、導電率に関し不均質な部分からなっている場合、イオンの移動によって誘電損失が現れるという立場から誘電損失を論じたものである。
Debyeの双極子理論は、誘電体を構成する極性分子、もしくは極性基が、外部印加電界によって配向させられる時、熱運動による(分子振動による)抵抗を受けることによって、極性分子の配向が電界の変化に追従できず、その結果として誘電体損失が発生するという見方による理論である。
電気回路において用いられるインダクタンス、キャパシタンス、抵抗などの受動素子は、一般に集中定数回路素子と呼ばれ、時間遅れがないとして取り扱われている。分布定数回路では、この集中定数素子が連続的に分布しているものとして取り扱う領域のものである。この代表的なものが信号の配線・伝送に用いる伝送線路(分布定数線路)と呼ばれるものである。線路が集中定数素子が一様に分布するとしたとき、線路を流れる電流(線路電流)と線路間あるいはグラウンド面と線路間の電圧(線路電圧)は、電信方程式とよばれる連立1次方程式で与えられる。この電信方程式はその名前が示すように空中に張った金属線路に電信符号(モールス符号)を送信するとき、電圧/電流の振る舞いを記述する式として回路論的な立場から導出され、古くから利用されてきた方程式である。電信方程式は電磁波論的にも導出でき、そのときの電磁界はTEM(transverse electromagnetic mode)モードと呼ばれるものであり、線路方向(伝送方向)には電磁界成分は存在せず、線路方向に垂直な横断面に存在する成分である。
伝送線路が多数の導体線路から成るとき、多導体線路(多線条線路)という。このときの電信方程式は線路系の1次定数(単位長当たりのインダクタンスやキャパシタンスなど)を行列表示した形式で拡張表現することができる。このときの電信方程式の解を求めるための一手段としてモード変換法がある。この手法では線路電圧と線路電流は実(自然)電圧や実(自然)電流を、仮想的な電圧と電流とに変換することであり、この仮想的な電圧・電流の組みはお互いに独立な組み合わせでなければならない。これを直交モードと称するが、電磁界の姿態(モード)と異なる意味合いであることに注意が必要である。この独立な組合せはグラウンド線を除く線路の数だけ存在し、その組合せも基本的には多数存在する。直交モードに分解して表現した電信方程式は単独線路の場合と同様に表現されるので、簡単に求められ、それらを再び組み合わすことで多導体線路での解が求められることになる。
2本の導体線路と基準線路あるいはグラウンド面からなる線路系は、多導体線路系の基本となる線路系である。この線路系の最もポピュラーな直交モードの組合せがEMCの分野ではディファレンシャルモードとコモンモードと呼ばれるものである。ディファレンシャルモード電流は、2本の線路を等量逆相で流れる成分であり、コモンモード電流は、同相で流れる成分である。マイクロ波回路の分野においては奇モードと偶モードと呼ばれるものが一般に使用されるが、実電圧/電流からモード電圧/電流への変換行列が異なり、したがって両モードの特性インピーダンス表現も異なる。
光線が従う変分原理をすべての出発点とする学問.光が進む路を追うことで,空間的に描き出された光線の幾何学データから光の入出力特性あるいは伝搬特性を議論する.光線光学ともよぶ.レンズの特性に特化した幾何光学をレンズ光学という.狭義の意味では光の波の界は含んでいないが,幾何光学の考察で容易に演繹される界は広義の解釈で含めることもある.光線の定義は群光線(エネルギー光線)であって位相光線(波面法線光線)でない.波面に付随する位相光線はここでの光線ではない.ただし真空中や等方性媒質中では両者が一致するため混用することがしばしばある.また幾何光学の基本原理はハミルトンの変分原理であって,位相光線に成立するフェルマーの原理ではない.しかし,このことも等方性媒質では両者の軌跡が一致するので,フェルマーの原理を幾何光学の原理としても差し支えない.群光線の挙動は力学の粒子運動(ニュートン運動)に酷似するため,光線の到達点における情報はすべて出発点の位置と方向で決まる.したがって,到達点における光の振る舞いは出発点の初期値で表現され,到達点の座標,方向,速度などは陽に含まない.考察が幾何学的であるため,直感的にわかりやすいが,光の回折効果は理論で排除されている.
微分方程式の厳密解がえられないときに表現する近似表現法のひとつ.解を小さいパラメータでべき級数展開し,その係数を,微分方程式から逐次決定する算法.パラメータと初項の選択に強く依存する.無限級数をそのまま計算すれば発散する「発散級数」となることがある.そのときでもパラメータが物理量のとき有限項も物理的意味をもち,また簡便な表示で良好な近似解がえられるので,多くの分野で重宝されている.物理でWKB法として知られるブリリュアンの解も典型的な発散漸近解である.一方,現在では特定の領域で発散しない級数も一様漸近展開といい,漸近展開に含められているが,特異性のない都合のよい解が得られる半面,精度の点で不満が残ることが多い.漸近展開は,1838年にエアリーが虹理論を提唱する際に用いた,いわゆるエアリー関数を,ストークスが既存の関数で表現しようとして失敗(1850),その結果として編み出した近似展開法.狭義の漸近展開法の命名は,後(1896)のポアンカレによる.